Effective Modern C++:Template and auto
The type deduction of Template and auto
The type deduction of template will ignore one level of reference and pointer
Example 1:
Input argument as reference
template<typename T>
void f(T& param);
int x = 27; // x is an int
const int cx = x; // cx is a const int
const int& rx = x; // rx is a reference to x as a const int
f(x);// T is int
f(cx);// T is const int, param's typeis const int&
f(rx);// T is const int, param's type is const int&
Example 2:
Input argument as pointer
template<typename T>
void f(T* param); // param isnow a pointer
int x = 27; // as before
const int *px = &x; // px is a ptr to x as a const int
f(&x); // T is int, param's typeis int*
f(px); // T is const int, param's type is const int*
Example 3:
Input argument as double reference, one will be ignored
template<typename T>
void f(T&& param); // param isnow a universal reference
int x = 27; // as before
const int cx = x; // as before
const int& rx = x; // as before
f(x); // x is lvalue, so T is int&, param's type is also int&
f(cx); // cx is lvalue, so T is const int&, param's type is also const int&
f(rx); // rx is lvalue, so T is const int&, param's type is also const int&
f(27); // 27 is rvalue, so T is int, param's type istherefore int&&
Example 4:
Input argument as value, cont and & will all be ignored
template<typename T>
void f(T param); // param is now passed by value
int x = 27; // as before
const int cx = x; // as before
const int& rx = x; // as before
f(x); // T's and param's types are both int
f(cx); // T's and param's types are again both int
f(rx); // T's and param's types are stillboth int
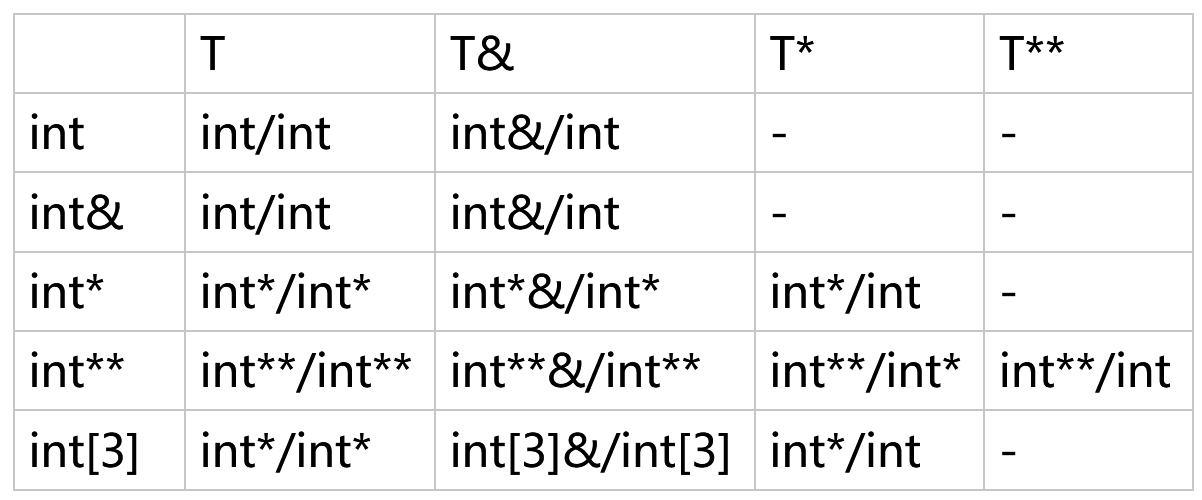
In the following table:
The type before / is the type of T
The type after / is the type of param