Graph Optimization 2 - Modelling Optimization Target

Usually, all graph optimization papers or tutorials start from raising the optimization problem: minimizing the following function:

\[F(x)=\sum_{ij}{e_{ij}(x)^T\Omega_{ij}e_{ij}(x)}\]

This article will explain where this optimization comes from and why it is related to Gaussian noise.

Maximum Likelihood Estimation with Gaussian noise

The probabilistic modeling of graph optimization is based on the Maximum Likelihood Estimation(MLE) algorithm. (More information on Chapter 6 of Xiang Gao’s book.).

The case we use for this article will also be the one we used in the last article:

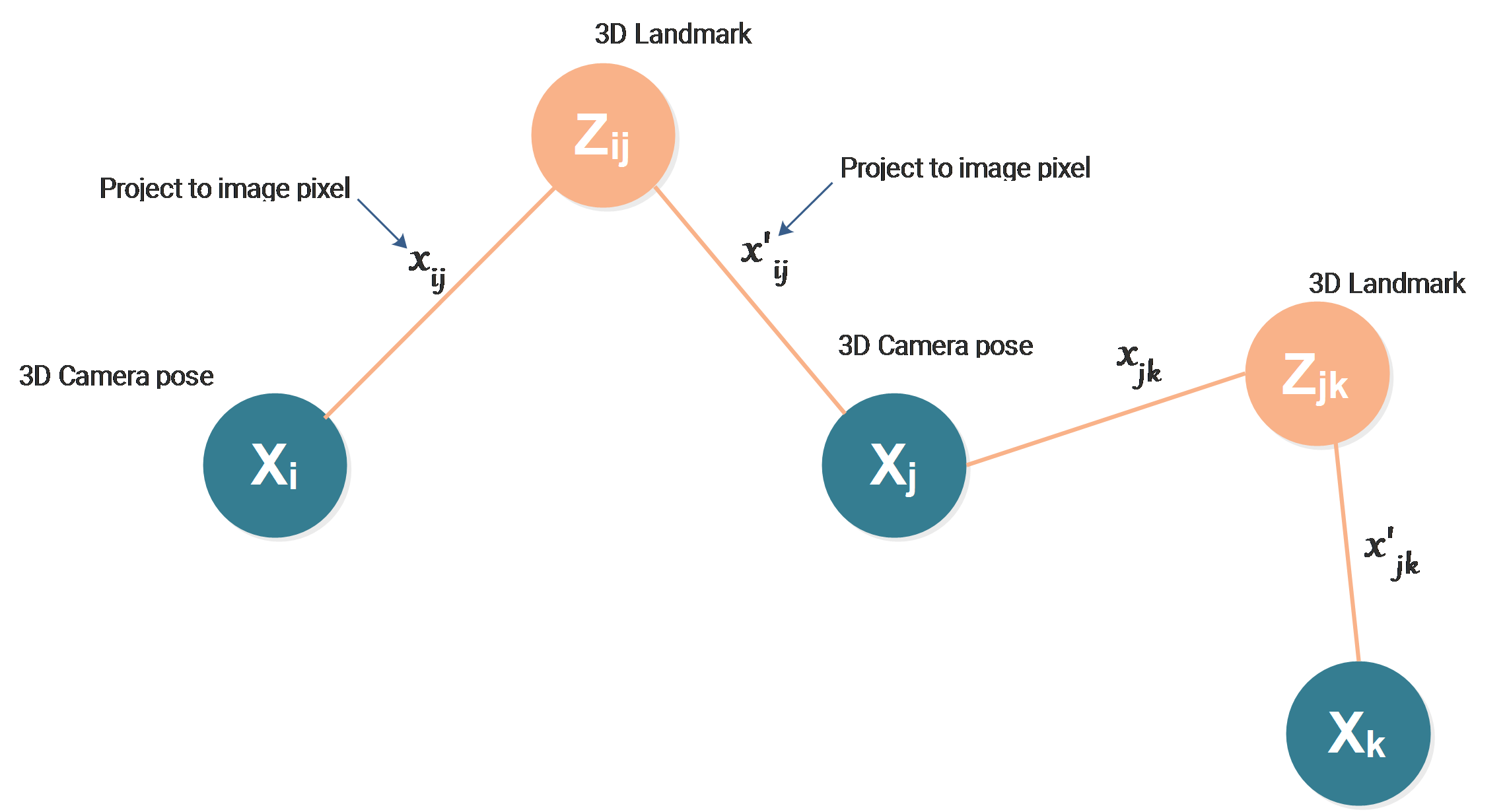
What we want to estimate are:

• Camera pose \(X_i\)
• Camera pose \(X_j\)
• 3D Landmark \(Z_{ij}\)

The 3D landmark can be seen by the camera at pose \(i\) and \(j\), the projections of the landmark on both cameras are our measurements:

• \(x_{ij}\) : 2D projection of \(Z_{ij}\) on camera at pose \(i\)

• \(x'_{ij}\) : 2D projection of \(Z_{ij}\) on camera at pose \(j\)

The basic idea of MLE is looking for the \(X_i,X_j\) and \(Z_{ij}\) to maximize the probability of getting the measurements \(x_{ij}\) and \(x'_{ij}\).

This probability is the so-called “likelihood”. Assuming that the noise we get in the measurement process is Gaussian noise, the probability can be modeled using Gaussian distribution.

Let’s say the projection of \(Z_{ij}\) onto the camera at pose \(X_i\) is a function \(Proj\):

\[\hat x_{ij}=Proj(Z_{ij},X_i)\]

The \(\hat x_{ij}\) is then the estimated measurement. The probability of getting the measured data \(x_{ij}\) is expressed as the likelihood between this estimation and the real measurement:

\[\mathcal{L}(x_{ij},\hat x_{ij})=\frac{1}{2\sigma_{ij}^2}e^{\displaystyle -\frac{(x_{ij}-\hat x_{ij})^2}{2\sigma_{ij}^2}}\]

Where \(\sigma_{ij}\) is considered the noise of our measurement.

Combining all the measurements together, we get:

\[\mathcal{L}=\prod{\mathcal{L}(x_{ij},\hat x_{ij})}=\prod{\mathcal{L}(x_{ij},Proj(Z_{ij},X_i))}\]

The problem turns to be maximize the above likelihood function:

\[\hat Z,\hat X= \displaystyle \arg \max_{X,Z}{\prod{\mathcal{L}(x_{ij},Proj(Z_{ij},X_i))}}\]

In order to get rid of the exponential root \(e\) and turn this maximization problem to be a minimization problem, we minimize the -log likelihood instead:

\[\hat Z,\hat X= \displaystyle \arg \min_{X,Z}{\{-log[\prod{\mathcal{L}(x_{ij},Proj(Z_{ij},X_i))]\}}}\]

then we get:

\[\hat Z,\hat X= \displaystyle \arg \min_{X,Z}{\{-\sum{log[\mathcal{L}(x_{ij},Proj(Z_{ij},X_i))]\}}}\]

After some calculation, we get:

\[\hat Z,\hat X= \displaystyle \arg \min_{X,Z}{\sum{\frac{1}{\sigma_{ij}^2}}(x_{ij}-Proj(Z_{ij},X_i))^2}\]

In the graph optimization convention, we define a new term:

\[\displaystyle \Omega_{ij}=\frac{1}{\sigma_{ij}^2},\]

this is the so-called “information” matrix. This information matrix \(\Omega_{ij}\) is a diagonal matrix, as usually the different dimensions of the measurement are independent.

The difference of real measurement and the estimated measurement is expressed as an error :

\[e_{ij}(x)=x_{ij}-Proj(Z_{ij},X_i),\]

where the new \(x\) represents all unknowns including \(X_i\) and \(Z_{ij}\).

\(e_{ij}(x)\) is taking care of the error related to \(X_i\) and \(Z_{ij}\) . For bundle adjustment, there is another error between \(X_j\) and \(Z_{ij}\):

\[e'_{ij}(x)=x'_{ij}-Proj(Z_{ij},X_j),\]

and there is also a:

\[\displaystyle \Omega'_{ij}=\frac{1}{\sigma _{ij}^{'2}},\]

We only use \(e_{ij}\) and \(\Omega_{ij}\) to represent both sides, just for convenience.

Don’t forget that all these parameters have many degrees of freedom, so they are actually vectors. Then our new \(x\) is also a vector. The negative log-likelihood turns to be:

\[F(x)=-log(\mathcal{L})=\sum_{ij}{e_{ij}(x)^T\Omega_{ij}e_{ij}(x)}\]

Now we converge to the convention of graph optimization, usually where every graph optimization starts from setting the optimization goal of minimizing:

\[F(x)=\sum_{ij}{e_{ij}(x)^T\Omega_{ij}e_{ij}(x)}\]