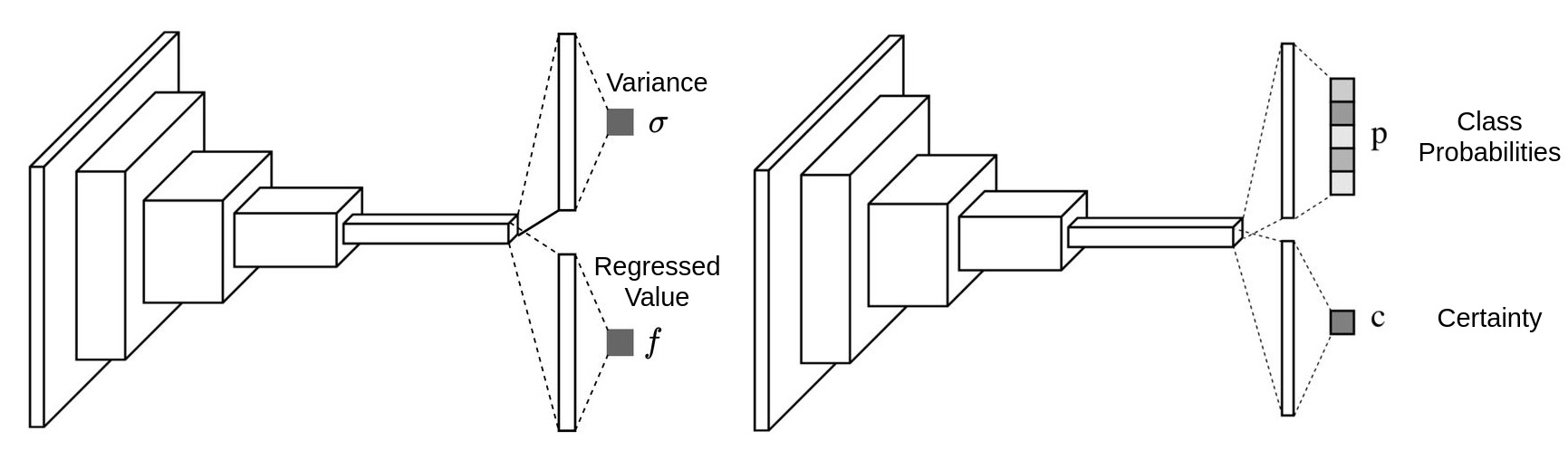
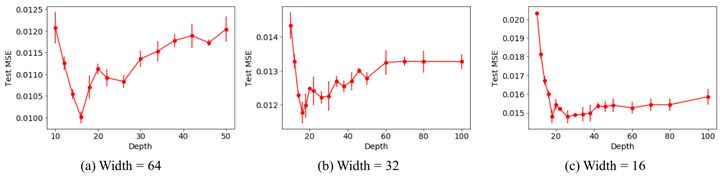
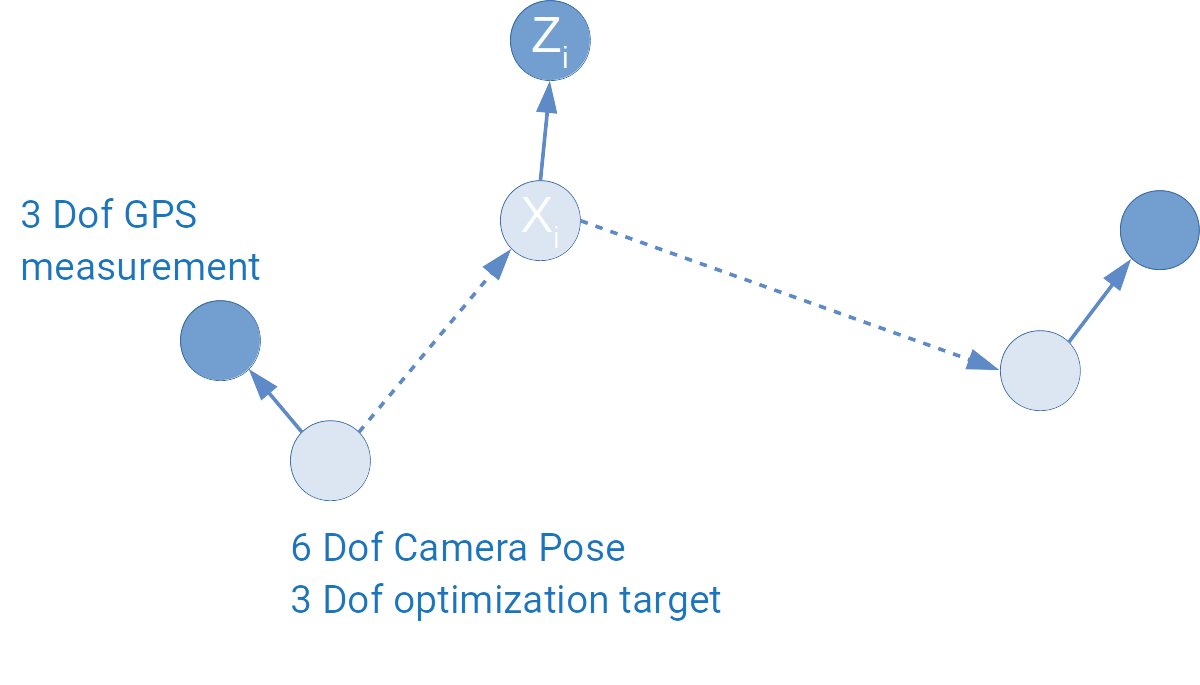
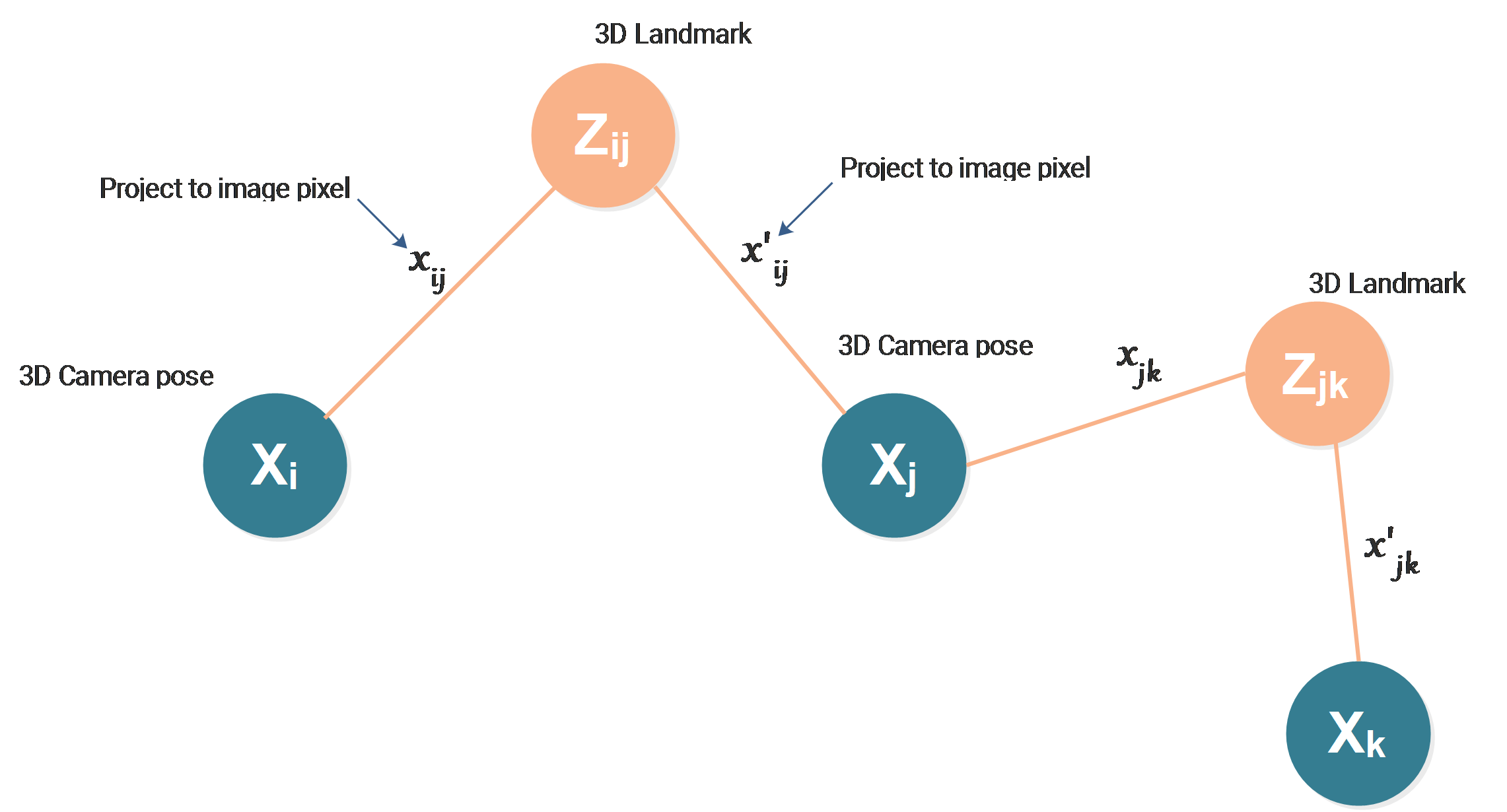
After two years of happy and constructive time in camera team, I got some homesick, I decided to go back to my 2nd hometown, Munich.
The days in Mobis are amazing. I learned so many new things and read so many papers that I can not even believe it, especially when I am cleaning them for the moving, Luka’s enthusiasm of new technologies motivated me to track the trend, which at end, benefits the design of our technical roadmap. The lessons I learned from Luka worth dual, maybe triple master degrees, one for geometry, one for deep learning and one for management, together with the lessons learned from everyone of camera team, I will definitely give myself an honored PhD title, awarded by camera team.
Before I joined camera team, I only have friends from few countries, now I have worked with the talents from so many countries and cultural backgrounds, the experience is unbelievably great. I got to understand so many cultures and religions, vividly, in person. My view of the world expanded so much here that I understand the world much more than before. The different cultures didn’t shock we, the diversity and the harmony of our team do amazed me. I would give special thanks to Thusita for constructing such a great team.
Conflicts and different technical views do exist, which is always helpful for us to regularize each other, I would consider these more as a kind of unsupervised learning. Thank you everyone for your tolerance on me, there are so many s**ty words came from my mouth and I am quite sure some of you guys definitely got ear pollution or even ear cancel.
I feel sad that I am leaving the camera team at this specific time, by doing good work, we win the trust from MTCK, we are working on more and more projects, we are moving to a bigger place and expanding further, last but not least, we just got a new lunch supplier!
It has been a great pleasure working with you all and I believe that we will have successful collaboration in the future!