The idea behind PCA
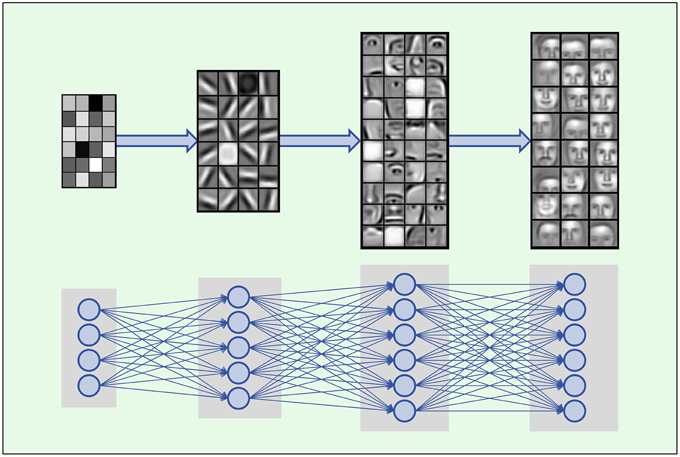
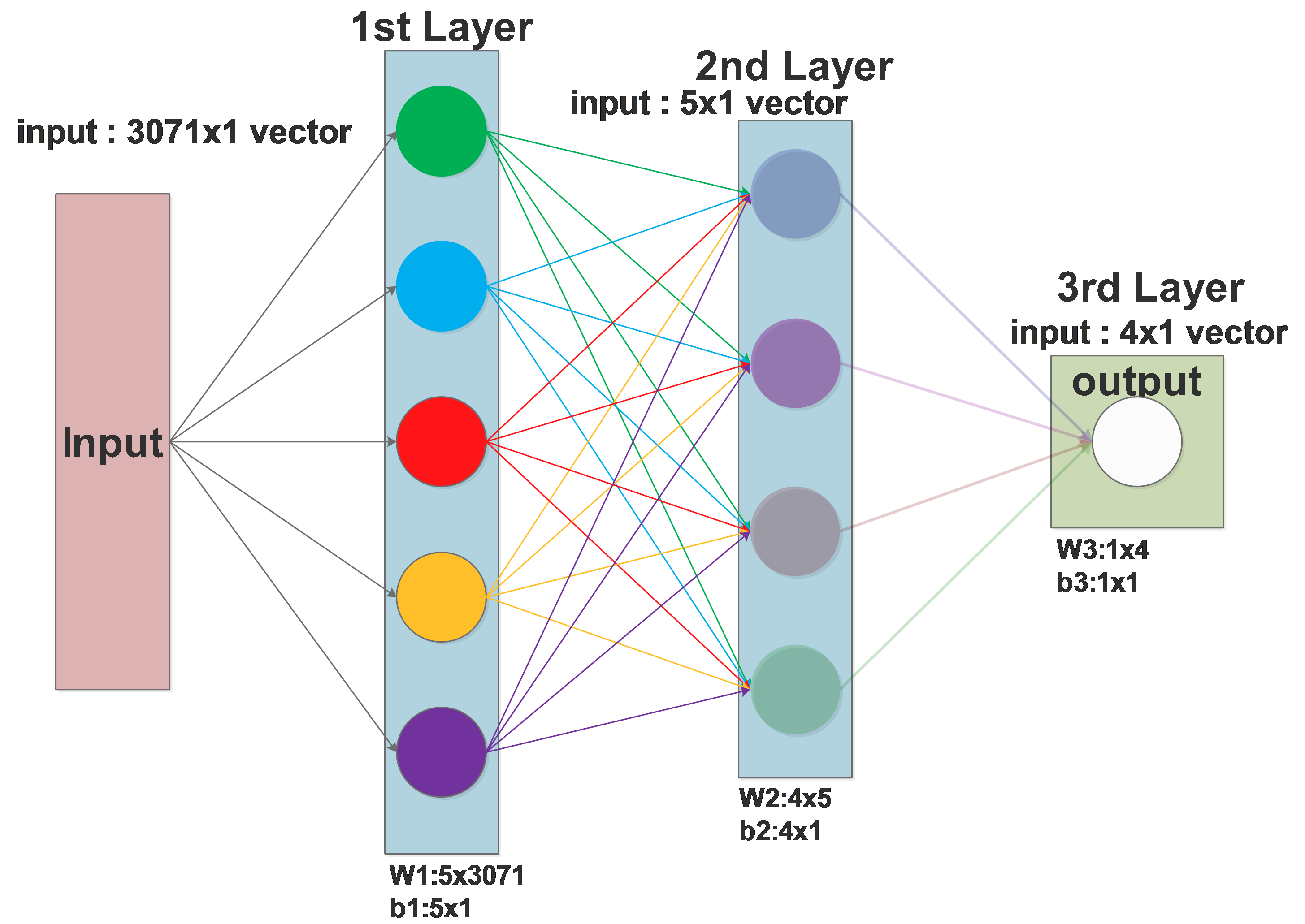
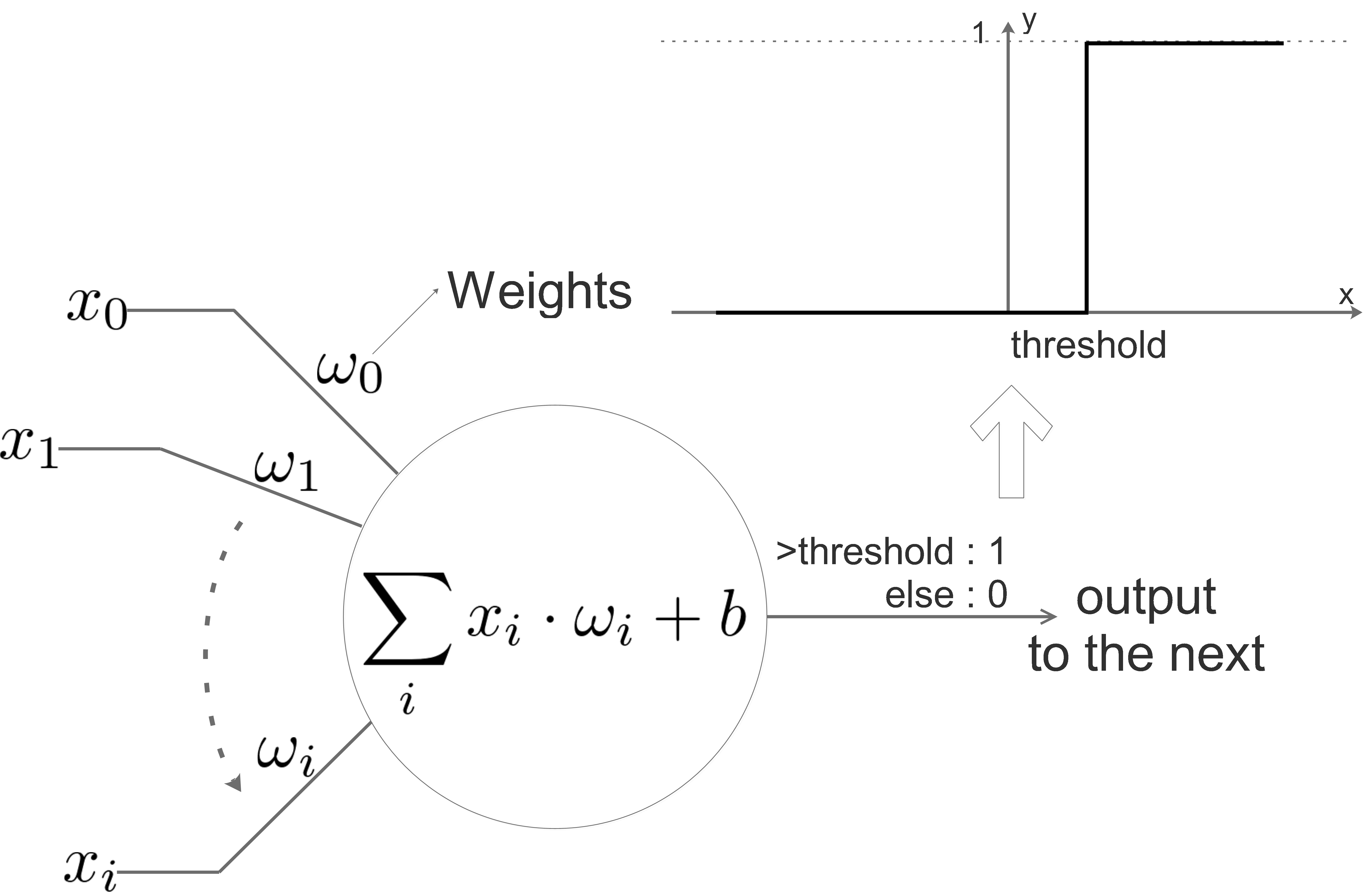
In the field of machine learning, PCA is used to reduce the dimension of features. Usually we collect a lot of feature to feed the machine learning model, we believe that more features provides more information and will lead to better result.
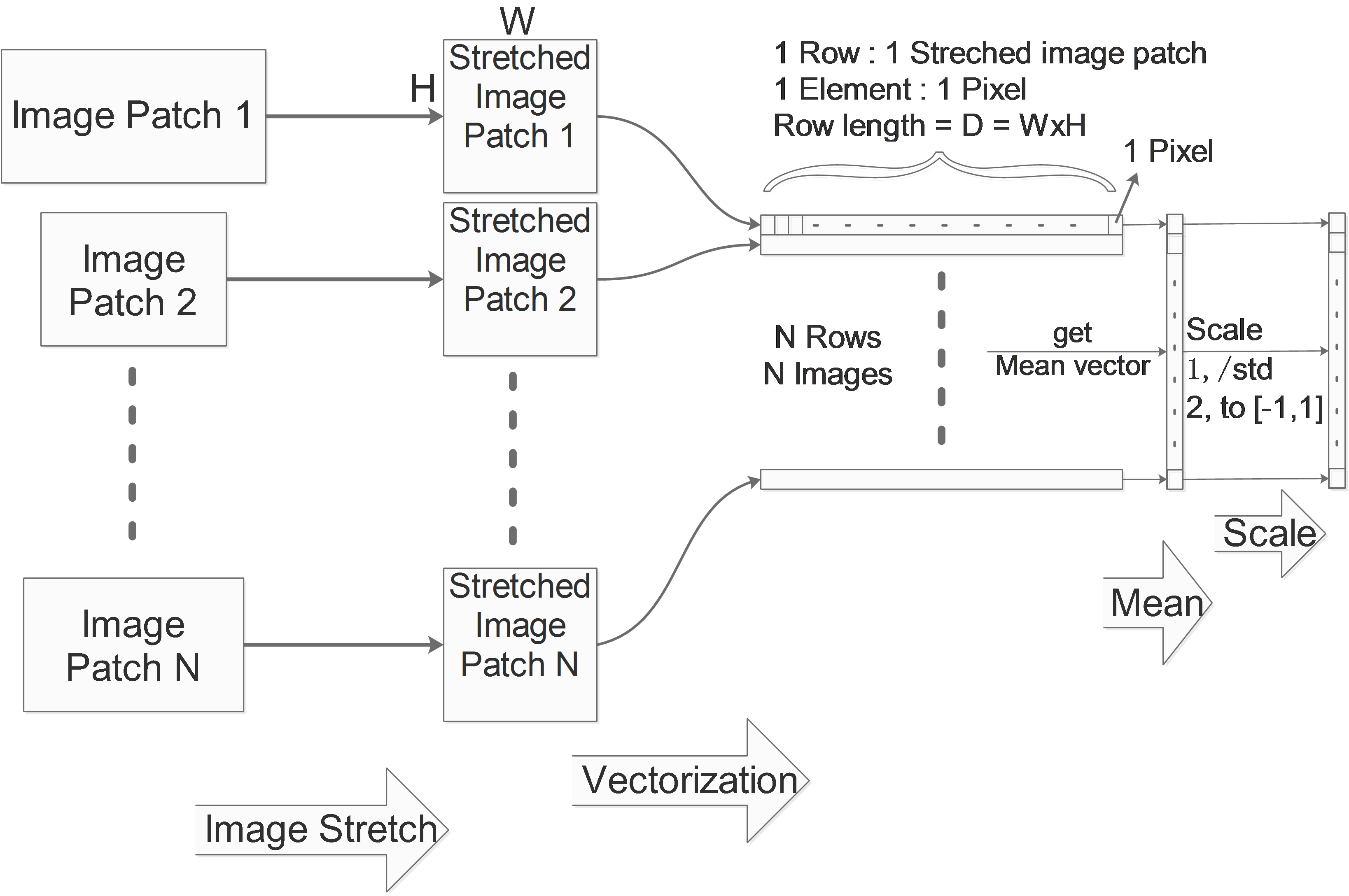
But some of the features doesn’t really bring new information and they are correlated to some other features. PCA is then introduced to remove this correlation by approximating the original data in its subspace, some of the features of the original data may be correlated to each other in its original space, but this correlation doesn’t exit in its subspace approximation.
Visually, let’s assume that our original data points \(x_1...x_m\) have 2 features and they can be visualized in a 2D space: