NN Backpropagation
The case we are handling: a 2 layers network
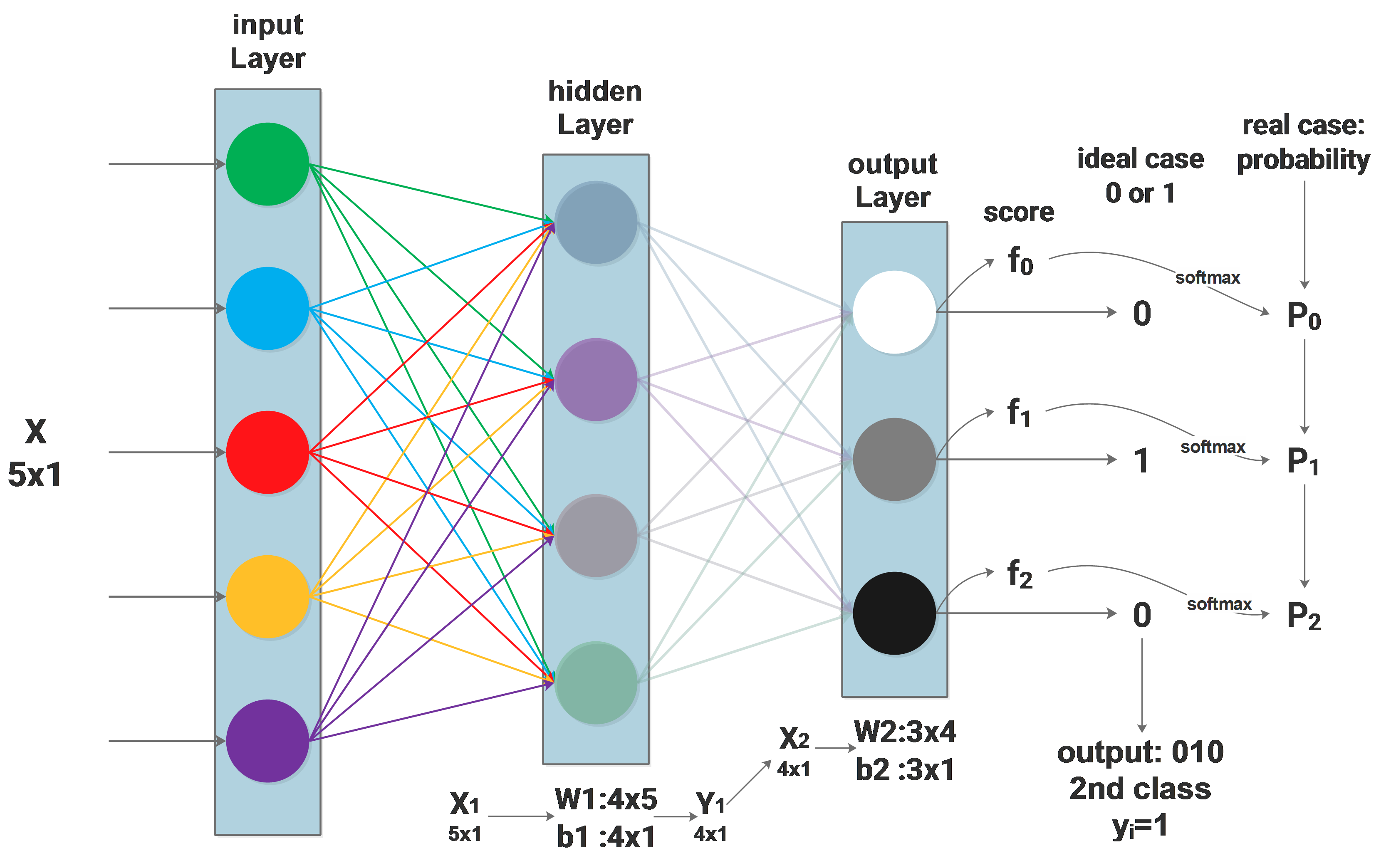
The above diagram shows the network to be used. From the last blog we get the loss function:
\[\mathscr{L}=arg\min_W\sum_i^N-log(\frac{e^{f_{y_i}}}{\sum\limits_j^Ce^{f_j}})\]In order to use the gradient descent algorithm to train \(\scriptsize W_1\) and \(\scriptsize W_2\), we need to compute the derivative of \(\scriptsize\mathscr{L}\) to \(\scriptsize W_1\) and \(\scriptsize W_2\), which are:
\[\frac{d\mathscr{L}}{dW_1}\space and\space \frac{d\mathscr{L}}{dW_2}\]If we have \(\scriptsize \frac{d\mathscr{L}}{dW_2}\) by hand, then \(\scriptsize W_2\) can be trained using gradient descent:
\[W_2^{i+1} =W_2^{i}-\lambda\Delta\frac{d\mathscr{L}}{dW_2^i}\]Compute $\frac{d\mathscr{L}}{dW_2}$
How to compute \(\scriptsize \frac{d\mathscr{L}}{dW_2}\)? We use the chain rule to “propagate back” the gradient, for \(\scriptsize W_2\):
\[\frac{d\mathscr{L}}{dW_2}=\frac{d\mathscr{L}}{df}\cdot \frac{df}{dW_2}\]As the last blog described, \(\scriptsize \frac{d\mathscr{L}}{df}\) of the \(\scriptsize ith\) sample can be expressed as:
\[\frac{\mathscr{dL}_i}{\mathscr{d}f_i}=\begin{cases} P_{y_i}-1\space\space\space\space for\space(j_i= y_i)\\ \\ P_{j_i}\space\space\space\space\space\space\space\space\space\space\space for\space(j_i\neq y_i) \end{cases}\]considering \(\scriptsize f=W_2\cdot X_2+b_2\):
\[\frac{df}{dW_2} = X_2\]then:
\[\frac{d\mathscr{L}}{dW_2}=\frac{\mathscr{dL}}{\mathscr{d}f} \cdot X_2\]Compute $\frac{d\mathscr{L}}{dW_1}$
Now we will compute \(\scriptsize \frac{d\mathscr{L}}{dW_1}\) to train \(\scriptsize W_1\). The gradient will be propagated back to \(\scriptsize W_1\) like this:
\[\frac{d\mathscr{L}}{dW_1}=\frac{d\mathscr{L}}{df}\cdot \frac{df}{dX_2}\cdot \frac{dX_2}{dY_1}\cdot \frac{dY_1}{dW_1}\]the same as before, we know that \(\scriptsize Y_1 = W_1\cdot X_1 + b_1\), the above equation results in:
\[\frac{d\mathscr{L}}{dW_1}=\frac{d\mathscr{L}}{df}\cdot W_2\cdot \frac{dX_2}{dY_1}\cdot X_1\]\(\scriptsize \frac{d\mathscr{L}}{df}\) is already known, \(\scriptsize \frac{dX_2}{dY_1}\) depends on the activation function of the hidden layer.
Using this method, we can easily propagate the gradient back to the input layer through the whole network and update all the layers, no matter how many layers are there in between.
