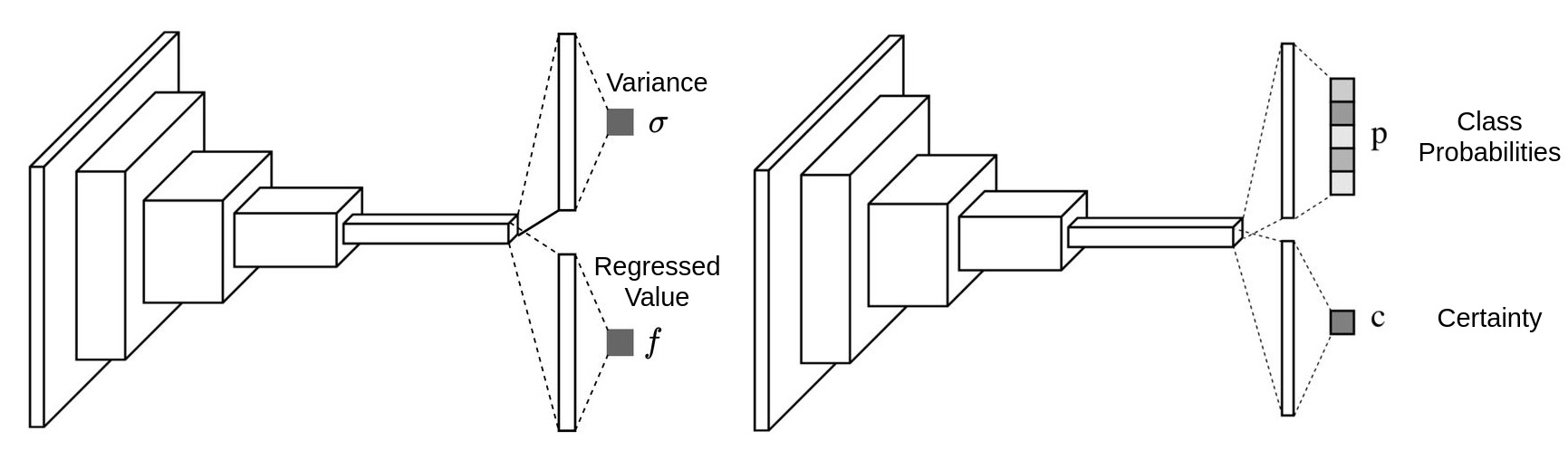
Theoretically, two layer neural network as an universal approximator can fit any random functions. We just need to increase the number of features of the hidden layer to make everything fitted. But the efficiency is very low.
Why deep
According to the paper Topology of deep neural networks, evey layer of a ReLU neural network is try to separate the data points by folding the high dimension manifold. The paper uses the Betti number to measure the distance between the current folded manifold and the final target manifold, it discovered that the works each layers have done are different for different networks.
For shallow networks, most of the folding efforts are done by the last layer. For deep networks, the folding efforts done by each layer are similar. Which means, the works done by each layer of a deep neural networks are relatively simple and easy, but the works to be done by the last layer of a shallow network are complicated and hard.
It is not hard to imagine, the deep neural network solves the problem by abstracting it, which makes the training easier and of higher efficiency.
The deeper, the better?
But it doesn’t mean the deeper is better, the paper Increasing Depth Leads to U-Shaped Test Risk in Over-parameterized Convolutional Networks shows that from the beginning depth really helps the neural network to get better, but once the depth passes a threshold, the network get worse:
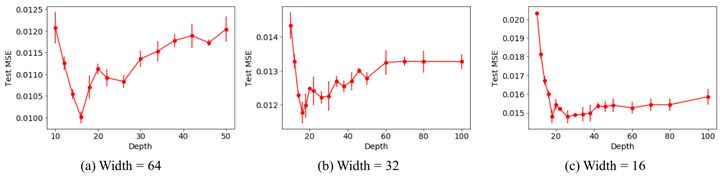
From the left to the right we can see how the test error changes with the change of depth on ResNets of different widths. Obviously, for whatever width, ResNet18 always achieves the best accuracy, and it gets worse after that.
We can understand it in a straight forward way: if the problem is simple, we should not over-abstract it, the networks will be confused by solving a simple problem with too many abstraction. On the other hand, if the problem is very hard, the network needs more layers of abstraction to solve it properly.